Random Forest es uno de los modelos de Machine Learning más conocidos y utilizados. Es un modelo que tiene muchas ventajas: sirve tanto para clasificación como regresión, es robusto a outliers, no tiende al overfitting, suele tener buena capacidad predictiva…. Es un gran modelo y, por ello, se usa mucho. Y muchas veces, sin saber cómo funciona.
Por eso, en este post te voy a explicar paso a paso cómo funciona Random Forest. Vamos a crear nuestro propio modelo de Random Forest desde 0. Y además vamos a probarlo en diferentes escenarios para que veas cómo se comporta y entiendas cómo de ciertas son algunas afirmaciones que se hacen sobre este modelo.
¿Te suena interesante? ¡Vamos con ello!
Introducción a Random Forest
Random Forest se basa en árboles de decisión. Por tanto, si quieres saber cómo funciona Random Forest, necesitas saber cómo funciona un árbol de decisión. Escribí en detalle sobre ello en este post, así que tranquilo, no me voy a detener demasiado en ello.
En cualquier caso, un aspecto importante a recordar es que los árboles de decisión eligen los splits (cortes) midiendo la impureza. Básicamente, prueban diferentes variables y diferentes formas de cortar con cada una de esas variables. De los dos grupos que genera el split se mide la impureza en cada uno de ellos y se calcula la impureza del corte como la media ponderada de la impureza de ambos grupos. Este proceso se realiza para todas las variables, se elige el split más puro y se vuelve a repetir.
Asimismo, los árboles de decisión tienen varios aspectos positivos:
- Sirven tanto para clasificación como regresión.
- Gestionan valores nulos.
- Son fácilmente entendibles, incluso por personas no técnicas.
Visto así parece que el árbol de decisión es un gran modelo. Sin embargo, tienen un problema principal, y es que en general no son eficaces: tienden al overfitting si no se podan o limita su crecimiento, pero cuando esto se hace, suelen tender al underfitting. De hecho, en el libro Elements of Statistical Learning (un libro muy reconodico en el mundo del Machine Learning) comentan lo siguiente: … Trees have one aspect that prevents them from being the ideal tool for predictive learning, namely inaccuracy.
Una forma que se pueden solucionar estos problemas de los árboles es aplicando técnicas de boosting o bagging. ADABoost, Gradient Boosting y XGBoost son ejemplos de árboles de decisión aplicando boosting. Random Forest, por su parte, es el resultado de aplicar teoría de bagging a árboles de decisión.
De árbol de decisión a bagging y a Random Forest
Bagging y problemas de aplicarlo a Árboles de decisión
El bagging es una técnica de machine learning, que consiste en crear muchos modelos, generalmente árboles o modelos pequeños o weak learners, para hacer la predicción como media de todos estos modelos.
Sin embargo, esto tiene un problema, y es que los árboles de decisión son modelos determinísticos, es decir, que si los ejecutas con los mismos datos y mismos parámetros, siempre conseguirás el mismo resultado. Esto se da porque ni su función de coste (la impureza) ni la forma de calcular splits tiene ningún componente aleatorio.
Aunque a nivel teórico los árboles de decisión son determinísticos, ciertas implementaciones, como la de Scikit-Learn no lo son, ya que se basan en ciertos procesos aleatorios para agilizar la ejecución. Puedes leer más sobre ello aquí.
Así pues, ¿cómo podemos conseguir crear varios árboles de decisión, entrenados sobre los mismos datos, y que devuelvan resultados diferentes? La única forma es conseguir que cada árbol sea diferente… y la única forma de conseguir eso, es que los datos con los que se entrena cada árbol sea diferente. Aquí es donde entra en juego el bootstrapping.
Boostrapping
El bootstrapping es una técnica estadística surgida en 1979 (enlace) que consiste en crear muchas muestras, del mismo tamaño que la población original, mediante muestreo aleatorio con reemplazo. En otras palabras: si tenemos una población de 1000 observaciones, vamos a crear muestras de 1000 observaciones. Para conseguir que dichas muestras sean diferentes, cada observación puede aparecer más de una vez en nuestra muestra. He creado la siguiente animación para que se entienda el proceso:

Y, todo esto, ¿para qué? Pues bien, gracias al bootstrapping contamos con muchas muestras diferentes sobre las que podemos trabajar, sin necesidad de tener que buscar más datos. Estas muestras nos pueden servir tanto como para estimar un estadístico como, en el caso de Random Forest, para entrenar un árbol de decisión.
Seguramente, si nunca has visto el bootstrapping en «acción», todo esto te suene raro. Aquí estamos para aprender así que… vamos a cer un ejemplo del funcionamiento del bootstrapping. Para ello, voy a crear datos aleatorios a partir de una distribución de chi cuadrado:
import numpy as np
import plotly.express as px
N_POULATION = 1000
np.random.seed(10)
population = np.random.chisquare(5, N_POULATION)
fig = px.histogram(
population,
title='Population Distribution',
template = 'plotly_white'
).update_layout(showlegend=False)
fig.show()
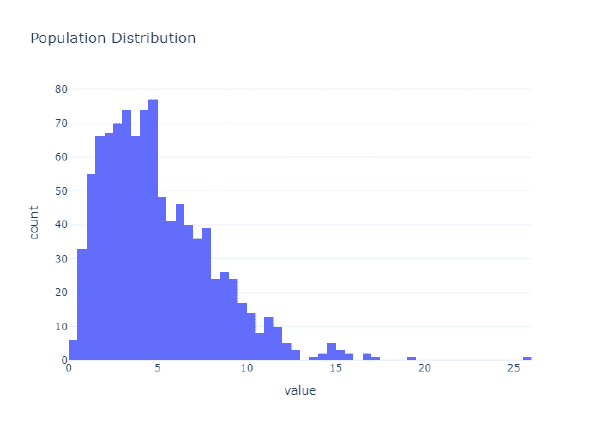
Estos son mi población, es decir, todos los datos que hay. Sin embargo, en la realidad no solemos tener accesible todos los datos, solo unos pocos. Así que, por ser fiel a la realidad, voy a coger una muestra aleatoria de dicha población. Voy a coger el 20% de los datos de forma aleatoria:
SAMPLE_PERCENT = .2
sample = np.random.choice(population, int(N_POULATION * SAMPLE_PERCENT))
fig = px.histogram(
sample,
title='Sample Distribution',
template = 'plotly_white'
).update_layout(showlegend=False)
fig.show()
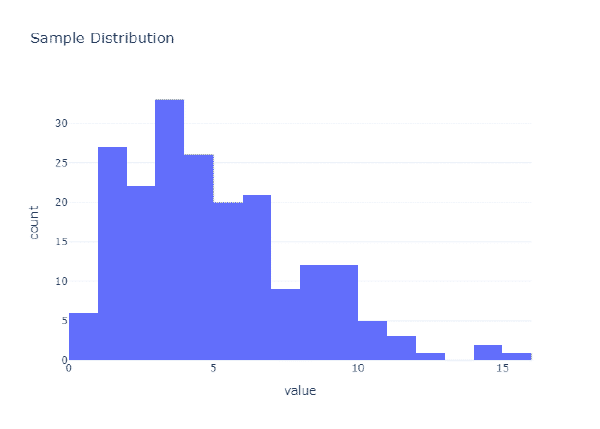
Como puedes ver, no es que las distribuciones sean las mismas. De hecho, si comprobamos diferentes estadísticos verás que, aunque los valores son parecidos, difieren un poco:
statistics = [
('mean', np.mean),
('median', np.median),
('std', np.std),
('q1', lambda x: np.percentile(x, 25)),
('q3', lambda x: np.percentile(x, 75))
]
for stat, f in statistics:
print(f'{stat} pop: {f(population):.2f}, sample: {f(sample):.2f}')
mean pop: 5.02, sample: 5.01
median pop: 4.44, sample: 4.49
std pop: 3.16, sample: 2.99
q1 pop: 2.65, sample: 2.70
q3 pop: 6.80, sample: 6.77
Pues bien, supongamos que queremos estimar la mediana. Para ello, podemos crear N muestras bootstrapped y calcular la desviación estándar en cada uno de estas muestras. Después, podemos estimar nuestro parámetro como la media de dichos estadísticos:
N_SAMPLES = 1000
# Calculate N bootstrap samples
def get_bootstrap_sample(sample: np.ndarray) -> np.ndarray:
return np.random.choice(sample, len(sample), replace=True)
# Get the bootstrap samples
samples = [get_bootstrap_sample(population) for _ in range(N_SAMPLES)]
# Calculate the statistic for each sample
boots_results = [np.median(samp) for samp in samples]
print(
f"Estimated median: {np.mean(boots_results):.2f}, "
f"Sample median: {np.median(sample):.2f}, "
f"Real median: {np.median(population):.2f}"
)
Estimated median: 4.43, Sample median: 4.49, Real median: 4.44
Como puedes ver, aplicando el cálculo estadístico sobre muestras bootstrapped hemos conseguido ser mucho más certeros en la estimación de nuestro estadístico real (4.43 vs 4.44) que aplicando el estadístico sobre toda la muestra (4.49 vs 4.44). Impresionante, ¿verdad? Y es que, en el fondo, gracias al bootstrapping podemos reducir el sesgo en nuestras estimaciones.
El bootstrapping no solo sirve para hacer estimaciones puntuales de estadísticos, con él también podemos calcular intervalos de confianza, p-values, etc. Sin embargo, no entraré en ello ya que no es un post sobre Bootstrapping, sino sobre Random Forest.
Bagging vs Árbol de Decisión
Podemos aplicar bootstrapping para crear diferentes datasets y, con cada uno de ellos, crear un árbol de decisión. Con esto tendríamos un sistema llamado bagging o bootstrapped aggregating. Este sistema seguramente mejore el funcionamiento de un árbol de decisión. De hecho, vamos a comprobarlo implementando nuestra clase de Bagging y comparando su rendimiento con los árboles de decisión.
from typing import List, Tuple
import numpy as np
import pandas as pd
from sklearn.base import BaseEstimator, ClassifierMixin
from sklearn.tree import DecisionTreeClassifier
from sklearn.utils import resample
from sklearn.utils.validation import check_is_fitted
class BaggingTreeClassifier(BaseEstimator, ClassifierMixin):
def __init__(self, n_estimators:int = 100):
self.n_estimators = n_estimators
def _create_bootstrapped_tree(
self, data:pd.DataFrame
) -> Tuple[pd.DataFrame, pd.DataFrame]:
boo_df = resample(data, n_samples=data.shape[0])
oob_df = data.loc[~data.index.isin(boo_df.index), :]
return boo_df, oob_df
def fit(self, X:pd.DataFrame, y:pd.Series):
self.estimators_:List[DecisionTreeClassifier] = []
self.oob_dfs_:List[pd.DataFrame] = []
for _ in range(self.n_estimators):
boo_df, oob_df = self._create_bootstrapped_tree(X)
estimator = DecisionTreeClassifier()
estimator.fit(boo_df, y.loc[boo_df.index])
self.estimators_.append(estimator)
self.oob_dfs_.append(oob_df)
return self
def predict(self, X:pd.DataFrame) -> np.ndarray:
check_is_fitted(self)
predictions = np.array([
estimator.predict(X) for estimator in self.estimators_
])
return np.mean(predictions, axis=0) > .5
Ahora vamos a cargar unos datos y comprobar qué tal funciona nuestro BaggingTreeClassifier. Para ello, vamos a utilizar el dataset de clasificación de cáncer de mama ofrecido por Scikit-Learn. Puedes aprender más sobre él aquí.
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix, accuracy_score
x, y = load_breast_cancer(return_X_y=True, as_frame=True)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = .4)
bag_tree = BaggingTreeClassifier()
bag_tree.fit(x_train, y_train)
preds = bag_tree.predict(x_test)
bagg_acc = accuracy_score(y_test, preds)
print(f'Bagging Accuracy: {bagg_acc:.2f}')
Bagging Accuracy: 0.96
Como vemos, el modelo parece funcionar bien a primera vista. Pero no sabemos si funciona mejor, peor o igual que un Árbol de Decisión.Así pues, para poder tener una imagen más fidedigna de cómo funciona el modelo, voy a entrenar un árbol de decisión normal:
En la realidad tendríamos que evaluar el modelo viendo la matriz de confusión y buscando reducir los falsos negativos en la detección de cáncer. Sin embargo, en este caso no buscamos el mejor modelo para el caso de uso, sino comparar el rendimiento.
dt = DecisionTreeClassifier()
dt.fit(x_train, y_train)
dt_preds = dt.predict(x_test)
dt_acc = accuracy_score(y_test, dt_preds)
print(f'Decision Tree Accuracy: {dt_acc:.2f}')
Decision Tree Accuracy: 0.92
Como vemos, entrenar muchos modelos de árboles de decisión sobe datasets bootstrapped ha conseguido mejorar la capacidad predictiva. Ahora demos un paso más, pasemos de un modelo de bagging a Random Forest.
De bagging a Random Forest
Aunque aplicando bagging se mejore el rendimiento de los árboles de decisión, aún se puede mejorar más. Vamos a pasar de un modelo de bagging a Random Forest. Y, para ello, simplemente hay que realizar un paso extra en nuestro modelo de bagging: en cada modelo, en vez de utilizar todas las variables disponibles, utilizaremos una cantidad de variables aleatoria.
De esta forma, cada árbol va a tener la misma cantidad de variables, pero estas no tienen por qué ser las mismas. Esto generará aún más diferencias entre los árboles, lo cual es beneficioso en términos de capacidad predictiva.
Así pues, vamos a crear nuestro modelo de Random Forest para ver qué tal funciona. Los principales cambios van a ser los siguientes:
- Crear un método llamado
_get_random_featuresque la cantidad de variables indicadas de forma aleatoria. - Aplicar el método
_get_random_featuresantes de llamar al método_create_bootstrapped_tree.
Nota: recuerda que esta clase es un ejemplo, no un estimador para usar en el día a día. Hay comprobaciones y cuestiones que dejo de lado para simplificar el código lo máximo posible.
class CustomRandomForestClassifier(BaseEstimator, ClassifierMixin):
def __init__(self, n_estimators:int = 100, max_features:int = 5):
self.n_estimators = n_estimators
self.max_features = max_features
def _create_bootstrapped_tree(
self, data:pd.DataFrame
) -> Tuple[pd.DataFrame, pd.DataFrame]:
boo_df = resample(data, n_samples=data.shape[0])
oob_df = data.loc[~data.index.isin(boo_df.index), :]
return boo_df, oob_df
def _get_random_features(
self, data:pd.DataFrame, max_features:int
) -> pd.DataFrame:
if max_features >= data.shape[1]:
raise ValueError(
'max_features must be less than the number of features'
)
return data.sample(max_features, axis=1)
def fit(self, X:pd.DataFrame, y:pd.Series):
self.estimators_:List[DecisionTreeClassifier] = []
self.oob_dfs_:List[pd.DataFrame] = []
self.oob_y_:List[pd.Series] = []
for _ in range(self.n_estimators):
df_sample = self._get_random_features(X, self.max_features)
boo_df, oob_df = self._create_bootstrapped_tree(df_sample)
estimator = DecisionTreeClassifier()
estimator.fit(boo_df, y.loc[boo_df.index])
self.estimators_.append(estimator)
self.oob_dfs_.append(oob_df)
self.oob_y_.append(y.loc[oob_df.index])
return self
def predict(self, X:pd.DataFrame) -> np.ndarray:
check_is_fitted(self)
base = tuple(zip(self.estimators_, self.oob_dfs_))
predictions = np.array([
estim.predict(X[df.columns]) for estim, df in base
])
return np.mean(predictions, axis=0) > .5
Ahora que ya tenemos la clase, vamos a ver qué tal funciona con el mismo ejemplo que hemos aplicado previamente:
rf = CustomRandomForestClassifier()
rf.fit(x_train, y_train)
rf_preds = rf.predict(x_test)
rf_acc = accuracy_score(y_test, rf_preds)
print(f'Random Forest Accuracy: {rf_acc:.2f}')
Random Forest Accuracy: 0.96
Asimismo, podemos comparar el funcionamiento del Random Forest que hemos creado con la implementación de Random Forest realizada en Scikit-Learn:
from sklearn.ensemble import RandomForestClassifier
sk_rf = RandomForestClassifier(
max_features=5, n_estimators=100, oob_score=True
)
sk_rf.fit(x_train, y_train)
sk_rf_preds = sk_rf.predict(x_test)
sk_rf_acc = accuracy_score(y_test, sk_rf_preds)
print(f'Sklearn Random Forest Accuracy: {sk_rf_acc:.2f}')
Sklearn Random Forest Accuracy: 0.96
Como vemos, nuestra implementación ha dado exactamente la misma capacidad predictiva que la clase de Scikit-Learn. Esto no es porque los dos modelos sean iguales, simplemente, por casualidad, por la forma que ambos se han inicializado. En cualquier caso, el punto es el siguiente: hemos creado un modelo de Random Forest desde 0 y, lo mejor de todo, es que no ha sido excesivamente complicado hacerlo.
Perfecto, ahora que conoces cómo funciona Random Forest, vamos a ir un poco más allá.
Comprobando creencias sobre Random Forest
A lo largo de los años he leído/escuchado a mucha gente hablar sobre Random Forest. De hecho, diría que existe una serie de cuestiones sobre Random Forest que la gente cree, pero que no necesariamente son ciertos. Se les poría llamar como los mitos de Random Forest.
En esta sección voy a comprobar algunos de dichos mitos para ver cómo de ciertos son y en qué medida lo son. Los mitos que voy a comprobar son los siguientes:
- Al ser un modelo de ensemble, Random Forest no sufre de overfitting.
- Random Forest, al estar basado en árboles, no se ve afectado por las variables correlacionadas.
- No hace falta comprobar sobre test un Random Forest para saber qué tal funciona.
Así pues, vamos a comprobar uno a uno cuánto de cierto tienen estos «mitos» sobre Random Forest. Vamos con ello.
¿Evita siempre el overfitting un Random Forest?
He leído/oído a varias personas comentar que un Random Forest es un muy buen modelo porque siempre evita el overfitting. Pero… ¿es eso cierto? Si lo piensas detenidamente, hay dos variables que afectan en este sentido:
- El número de áboles que creas.
- La complejidad del dataset. La complejidad de un dataset no es algo que puedas medir de forma sencilla, pero podemos entender que cuantas más observaciones, más complejo puede ser un dataset.
Así pues, vamos a hacer el siguiente experimento: vamos a ver la diferencia en tasa de acierto en train y test para diferentes tipos de datasets y diferente número de árboles creados. De esta forma, podremos ver a partir de qué punto Random Forest deja de sufrir de overfitting.
Así pues, vamos a crear diferentes datasets con diferente número de observaciones. Para cada uno de ellos, entrenaremos Random Forest con diferente cantidad de árboles y finalmente veremos cuál de ellos funciona mejor.
Para facilitar el proceso, voy a empzar creando una función que recibe unos datos, hace el split entre tain y test, entrena Random Forest y calcula la métrica objetivo:
import numpy as np
def _get_rf_metrics(
x:np.array, y:np.array, n_estimators:int=100
) -> Tuple[float, float]:
x_train, x_test, \
y_train, y_test = train_test_split(x, y, test_size=.2)
rf = RandomForestClassifier(n_estimators=n_estimators)
rf.fit(x_train, y_train)
preds = rf.predict(x_test)
train_acc = accuracy_score(y_train, rf.predict(x_train))
test_acc = accuracy_score(y_test, preds)
return train_acc, test_acc
Ahora que tenemos la función, vamos a crear una serie de datasets, cada uno con diferente cantidad de observaciones. Además, crearemos modelos con diferente cantidad de árboles, para ver cómo se comportan. Vamos con ello:
Este bloque de código lleva bastante tiempo de ejecución y únicamente tiene como intención generar el código más adelante. Así pues, no recomiendo que lo ejecutes.
from sklearn.datasets import make_classification
N_TREES:List[int] = [100, 500, 1000]
N_FEATURES:List[int] = [5, 10, 20]
N_SAMPLES:List[int] = (
np.exp(np.linspace(np.log(100), np.log(1e5), 10))
.astype(int).tolist()
)
results = []
for sample in N_SAMPLES:
x, y = make_classification(n_samples=sample)
for trees in N_TREES:
ac_train, ac_test = _get_rf_metrics(x, y, n_estimators=trees)
results.append({
'n_samples': sample,
'n_trees': trees,
'train_acc': ac_train,
'test_acc': ac_test
})
Ahora que hemos ejecutado todo, vamos a visualizar los resultados a ver cómo se comporta:
import plotly.express as px
import pandas as pd
res_df = pd.DataFrame(results)
fig = (
res_df
.melt(id_vars=['n_samples', 'n_trees'])
.sort_values(['n_samples', 'n_samples'])
.pipe(
px.line,
x = 'n_samples',
y = 'value',
color = 'variable',
facet_col = 'n_trees',
template = 'plotly_white',
title = "Train vs Test Accuracy Evolution"
)
.update_layout(
legend_title = '',
legend={
"orientation": "h",
# yanchor="top",
"xanchor": "right",
"x": 1,
}
)
)
fig.show()
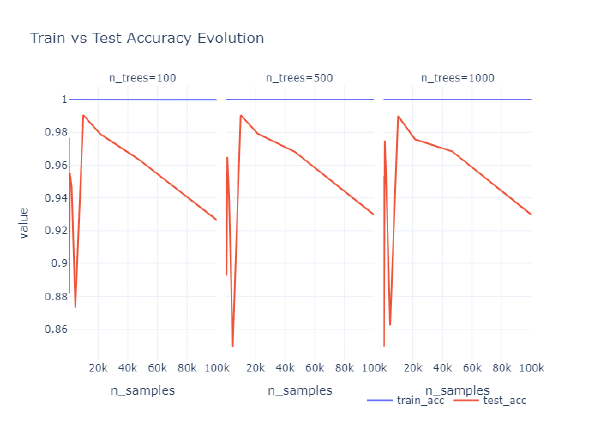
Como podemos ver, independientemente del número de estimadores que usemos, en este caso, siempre pasa lo mismo: a partir de 20k observaciones, el resultado en train se mantiene, pero en test baja. En resumen: en este caso, estamos sufriendo de overfitting.
Sí, las razones pueden ser varias (un dataset simple, pocas variables, muchas observaciones parecidas…) pero eso no es lo importante. Lo importante es desmentir que, efectivamente, con un modelo de Random Forest se puede sufrir overfitting. Sí, quizás es más complicado que con otro tipo de modelos, pero aun así, puede llegar a darse. Y, por tanto, es algo que debe comprobarse y, en caso de darse, atajarlo.
De cara a atajarlo, existen diferentes formas de hacerlo:
- Modificar los hiperparámetros del Random Forest, es decir, crear menos árboles y/o usar menos variables en cada uno de ellos.
- Modificar los hiperparámetros de los árboles subyacentes al Random Forest, como la profundidad máxima de dichos árboles o el número de observaciones para hacer splits.
- Modificar los datos con los que se entrena el modelo, obteniendo más datos, comprobando que no exista data leakage u obteniendo mayor proporción de variables relevantes.
Desmentido este mito, vamos a comprobar el siguiente.
Random Forest no se ve afectado por variables correlacionadas
Al crear diferentes árboles, cada uno de ellos con diferentes variables, se cree que el hecho de tener variables correlacionadas se ve muy diluido. Y es que, dichas variables correlacionadas no tienen por qué estar en todos los árboles.
Así pues, para comprobarlo, vamos a realizar la siguiente prueba:
- Vamos a partir de un dataset conocido.
- Vamos a crear N cantidad de nuevas variables que estén correlacionadas en un Y porciento con una de las variables originales.
- Entrenaremos un modelo y obtendremos su rendimiento en test para ver qué tal funciona.
- Graficaremos los resultados.
Así pues, lo primero de todo va a ser crear una función que, dados unos datos, una cantidad de variables y un grado de correlación, cree nuevas variables correlacionadas con la antiguas.
La explicación matemática de la función a continuación la puedes encnontrar aquí, yo simplemente he traducido el código de R a código de Python.
from sklearn.datasets import load_diabetes
from scipy.linalg import qr
x, y = load_diabetes(return_X_y=True, as_frame=True, scaled=False)
x = x.drop(columns = 'sex')
def generate_correlated_values(
data:pd.Series,
correlation:float = .8
) -> Tuple[np.array, float]:
n = data.shape[0]
rho = np.clip(correlation, -1, 1)
# corresponding angle
theta = np.arccos(rho)
# new random data
x2 = np.random.normal(2, .5, n)
# matrix
X = np.column_stack((data, x2))
# centered columns (mean 0)
Xctr = X - X.mean(axis=0)
# identity matrix
Id = np.eye(n)
Q, _ = qr(Xctr[:, [0]], mode='economic')
P = Q @ Q.T
x2o = (Id - P) @ Xctr[:, 1]
norms = np.sqrt((Xctr**2).sum(axis=0))
norms[norms == 0] = 1
Xc2 = np.column_stack((Xctr[:, 0], x2o))
Y = Xc2 / norms
x = Y[:, 1] + (1 / np.tan(theta)) * Y[:, 0]
correlation = np.corrcoef(data, x)[0, 1]
return x, correlation
new_col, cor = generate_correlated_values(x['s1'], correlation=.8)
print(f'Correlation: {cor:.2f}')
fig = px.scatter(
x = x['s1'],
y = new_col,
title = 'Correlated Data',
template = 'plotly_white'
)
fig.show()
Correlation: 0.80
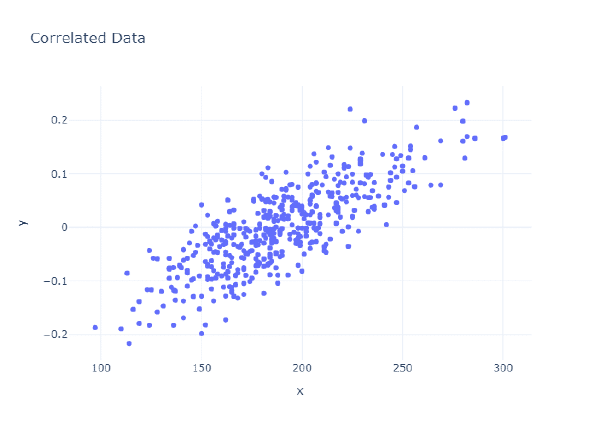
Como puedes ver, la nueva variable está correlacionada en el grado que queríamos. Genial. Teniendo esto, ahora vamos a crear un una nueva función que genere un dataset con todas las variables correlacionadas en una medida con las variables originales:
def generate_correlated_data(
data:pd.DataFrame,
correlation_levels:list[float]
) -> dict:
results = {}
for correlation in correlation_levels:
df = pd.DataFrame()
for col in data.columns:
new_col, _ = generate_correlated_values(data[col], correlation)
df[f'{col}_corr'] = new_col
results[correlation] = df
return results
# Get correlated data
CORRELATIONS = np.linspace(.1, 1, 20).round(2).astype(float).tolist()
CORRELATIONS[-1] = .99
corr_dfs = generate_correlated_data(x, CORRELATIONS)
# Check the correlation
for col in x.columns:
real_correlation = np.corrcoef(
x[col], corr_dfs[0.1][f'{col}_corr']
)[0, 1]
print(
f'{col} : '
f'Expected correlation: {CORRELATIONS[0]} - '
f'Real correlation: {real_correlation:.2f}'
)
age : Expected correlation: 0.1 - Real correlation: 0.10
bmi : Expected correlation: 0.1 - Real correlation: 0.10
bp : Expected correlation: 0.1 - Real correlation: 0.10
s1 : Expected correlation: 0.1 - Real correlation: 0.10
s2 : Expected correlation: 0.1 - Real correlation: 0.10
s3 : Expected correlation: 0.1 - Real correlation: 0.10
s4 : Expected correlation: 0.1 - Real correlation: 0.10
s5 : Expected correlation: 0.1 - Real correlation: 0.10
s6 : Expected correlation: 0.1 - Real correlation: 0.10
Como podemos ver, todas las variables están correlacionadas en el grado que esperamos. Así pues, ahora vemos a crear diferentes datasets, cada uno de ellos con diferente cantidad de variables correlacionadas y grados de correlación. Además, vamos a añadir los datos originales (con correlación 0), para poder comparar de forma más fácil cómo se comporta el modelo con datos correlacionados vs sin datos correlacionados.
Por cuestiones de visualización, en lugar de entrenar los dator originales 1 vez, los incluiré 1 vez por cada nº de variables que estoy probando.
import itertools
N_COLS:list[int] = list(range(1, x.shape[1] + 1))
# Get all the combinations
comb = list(itertools.product(CORRELATIONS, N_COLS))
# Generate the dataframes
cor_dfs = [corr_dfs[cor].iloc[:,:n_col] for cor, n_col in comb]
# Add the cor to the original data
dfs = [pd.concat([x, cor_df], axis = 1) for cor_df in cor_dfs]
dfs = [x] + dfs
comb = [(0, 1)] + comb
len(dfs)
181
Ahora que tenemos todas las combinaciones (160 en total), vamos a realizar una prueba, para cada una de ellas voy a generar un Random Forest, y obtendré el rendimiento en test. Guardaré tanto los valores de input del modelo como el rendimiento del modelo:
from sklearn.metrics import mean_squared_error
from functools import lru_cache
def check_rf(
x:pd.DataFrame, y:pd.Series, training_index:list[int]
) -> float:
x_train = x.loc[training_index, :]
x_test = x.loc[~x.index.isin(training_index), :]
y_train = y.loc[training_index]
y_test = y.loc[~y.index.isin(training_index)]
rf = RandomForestClassifier()
rf.fit(x_train, y_train)
preds = rf.predict(x_test)
return float(mean_squared_error(y_test, preds))
Ahora que tenemos la función, vamos a usarla para entrenar un modelo con cada uno de ellos y obtener el error del mismo. Además, entrenaremos todo tres veces para tener resultados más sólidos.
N_RUNS:int = 3
results = []
for run in range(N_RUNS):
training, _ = train_test_split(x, test_size=.2)
res = [check_rf(df, y, training.index) for df in dfs]
results.append(res)
Finalmente, vamos a graficar los valores. Para que sea más fácil de interpretar, voy a coger la ejecución sobre datos sin correlación como base y calcular el error en base al resultado obtenido:
fig = (
pd.DataFrame(comb* 3, columns = ['correlation', 'n_cols'])
.assign(mse = list(itertools.chain(*results)))
.groupby(['n_cols', 'correlation'])
.mean()
.reset_index()
.assign(
base = lambda x: x.query('correlation == 0')['mse'][0],
performance = lambda x: 100 * ((x['mse'] / x['base']) - 1)
)
.drop(['base', 'mse'], axis = 1)
.query("correlation > 0")
.pivot(index='n_cols', columns='correlation', values='performance')
.reset_index()
.assign(
percent_cols = lambda x: round(100 * x['n_cols'] / x['n_cols'].max())
)
.drop('n_cols', axis = 1)
.set_index('percent_cols')
.round(2)
.sort_index(ascending=False)
.pipe(
px.imshow,
aspect="auto",
text_auto=True,
origin='lower',
title = (
"Random Forest Performance<br><sup>"
"Dending on Correlation Level and Nº of Correlated "
"Features</sup>"
)
)
)
fig.show()
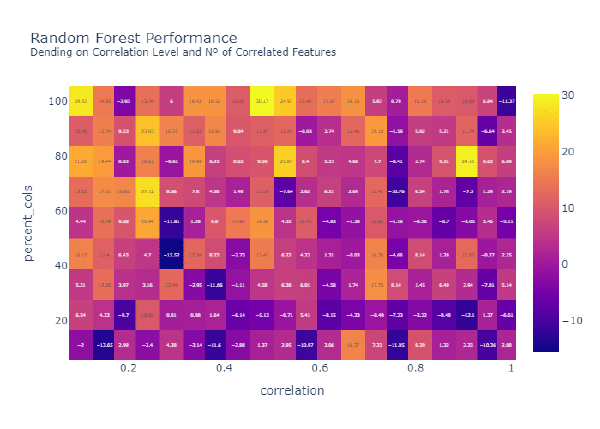
Del siguiente gráfico podemos sacar las siguientes conclusiones:
- Independientemente del nivel de correlación, si el porcentaje de variables correlacionadas sobre el total es bajo, el rendimiento del modelo se ve degradado en comparación con el modelo sin variables correlacionadas.
- A medida que aumenta el porcentaje de variables correlacionadas, la capacidad predictiva del modelo no se ve afectada. De hecho, el rendimiento del modelo ha mejorado, aunque esto es probable que sea derivado de la aleatoriedad, y no un hecho del modelo en sí.
En definitiva, no podemos afirmar que un modelo de Random Forest no se vea afectado por variables correlacionadas. Sí se ve afectado, sobre todo cuando el número de variables correlacionadas (respecto al total de variables sin correlación) es bajo. Quizás Random Forest se vea menos afectado que otros modelos, pero , en cualquier caso, se ve afectado.
Cómo obtener una estimación del funcionamiento del modelo sin test e impacto en rendimiento
Este punto, más que una creencia, es un hecho. Sí, has leído bien: con Random Forest podemos hacernos una idea general de cómo de bien (o mal) funciona el modelo, sin tener que utilizar el dataset de test. Esto puede ser interesante, únicamente, cuando cuentas con pocos datos y separar entre train y test te lleve a tener aún menos datos. En este caso, puede ser buena idea usar Radom Forest sobre el total del dataset y usar el OOB error para tener una idea del rendimiento del modelo.
Aunque el caso previo sea interesante, personalmente siempre creo que es prioritario conseguir más datos a utilizar este tipo de técnicas. En cualquier caso, lo explico para que conozcas que es posible, aunque no sea recomendable.
Y es que, cuando creas los dataset bootstrapped, ocurren dos cosas:
- Hay observaciones que aparecen más de una vez en el dataset bootstraped.
- Hay observaciones que no aparecen en el dataset bootstraped.
Estas segundas observaciones se conocen como Out of Bag Dataset (OOB Dataset). En el fondo son observaciones con las que ese estimador en concreto no se ha entrenado. Así pues, podemos estimar el funcionamiento de Random Forest viendo cómo funciona en el OOB dataset. A este error se le conoce como Out of Bag Error (OOB Error).
Vamos a calcular el OOB error con el estimador que hemos creado (lo ideal sería que este código se incluyera en un método de la clase, pero no lo he hecho para no hacer la clase muy larga ni poner código que explicaré más adelante):
errors = []
for i, _ in enumerate(rf.estimators_):
est = rf.estimators_[i].predict(rf.oob_dfs_[i])
oob_error = accuracy_score(rf.oob_y_[i], est)
errors.append(oob_error)
print(f"OOB Error: {np.mean(errors) :.2f}")
OOB Error: 0.89
Como vemos, efectivamente el OOB error devuelve un valor bastante similar al que nosotros tenemos en test. En el caso de usar la implementación de Random Forest de Scikit-Learn, puedes obtener el OOB error siempre y cuando, al entrenar, fijes el parámetro oob_score = True. La forma de obtenerlo es con el atributo oob_score_:
print(f"OOB Score: {sk_rf.oob_score_:.2f}")
OOB Score: 0.95
¿Qué diferencias hay entre entrenar con y sin OOB? Básicamente, si definimos que se calcule el OOB, esto lleva una computación adicional durante el proceso de fit, lo cual puede llevar algo de tiempo. En datasets normales esto no debería suponer una gran diferencia en términos de rendimiento, pero seguramente el tiempo de ejecución aumente a medida que aumenta el dataset.
De hecho, lo vamos a comprobar a ver a partir de qué punto existen las divergencias. Para ello, lo primero voy a crear una función para comprobar el tiempo de ejecución de cada modelo:
import time
def get_rf_fit_time(x, y, oob_score:bool):
rf = RandomForestClassifier(oob_score=oob_score)
start = time.time()
rf.fit(x, y)
end = time.time()
return end - start
from sklearn.datasets import make_classification
from tqdm import tqdm
N_SAMPLES = (
np.exp(np.linspace(np.log(100), np.log(1e6), 20))
.astype(int).tolist()
)
results = []
for sample in tqdm(N_SAMPLES):
x, y = make_classification(n_samples = sample)
fit_time = get_rf_fit_time(x, y, True)
results.append((sample, fit_time, True))
fit_time = get_rf_fit_time(x, y, False)
results.append((sample, fit_time, False))
import plotly.express as px
res_df = pd.DataFrame(
results,
columns=['n_samples', 'fit_time', 'oob_score']
)
fig = px.line(
res_df,
x='n_samples',
y = 'fit_time',
color='oob_score',
template= 'plotly_white',
title = "OOB Impact on Fit Time"
)
fig.update_layout(
legend_title="",
legend={
"orientation": "h",
# yanchor="top",
"xanchor": "right",
"x": 1,
}
)
fig.show()
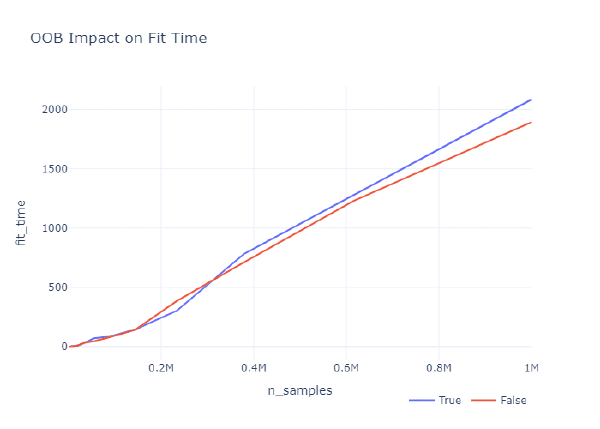
Como vemos, si trabajamos con menos de 500k observaciones, el impacto en el tiempo de entrenamiento entre calcular el OOB Error y no hacerlo es prácticamente nulo. Sin embargo, a partir de las 500k observaciones, el impacto empieza a incrementarse. De hecho, cuando trabajamos con datasets muy grandes, de más de 1 millón de observaciones, el impacto ya es considerable, siendo la diferencia en el tiempo de entrenamiento de alrededor de 3 minutos.
Así pues, como regla general si trabajas con pocas observaciones, que es cuando puede interesar usar OOB, puedes calcular el OOB. Pero si trabajas con muchas observaciones, no veo ningún motivo claro para calcular el OOB, ya que no aporta beneficios, pero incrementa el tiempo (y coste) computacional.
Conclusión y puntos clave de Random Forest
A modo de resumen, sin duda alguna Random Forest es un gran modelo, un modelo que todo data scientist debe conocer en profundidad. A mí, personalmente me encanta, porque aplicando dos técnicas muy sencillas (bootstrapping de los datos y selección aleatoria de las variables), supera varias de las limitaciones de los árboles de decisión. Me parece un modelo sencillo y elegante.
Sin embargo, esto no quiere decir que sea un modelo perfecto ni que funcione bajo toda circunstancia. Aunque se vea menos afectado que otros modelos por entrenar sobre un dataset con variables correlacioandas o sea más difícil de hacer overfitting con este modelo, ambas cuestiones pueden darse.
Así pues, es un mdoelo que puede utilizarse. De hecho, seguramente puede que sea uno de tus modelos go-to. Sin embargo, no se debe hacer una excepción con él. El proceso de limpieza de variables, comprobación de correlaciones (no únicamente lineales), fine-tuning de hiperparámetros, etc. debe hacerse como si de un modelo más sencillo se tratara.
Finalmente, ten en cuenta el OOB. Si trabajas con pocos datos, no utilizar un dataset de test y comprobar el performance con OOB puede ser una opción. Una opción que personalmente intentaría evitar,pero que ahí está. Asimismo, si el tiempo de entrenamiento es un limitante, puedes reducirlo no calculando el OOB. Si no lo necesitas, no lo incluyas.