SHAP Values: Explicabilidad de modelos de ML en Python

Los SHAP values es una de las técnicas de explicabilidad de modelos (Explainable AI) más conocidas y utilizadas. En este artículo, quiero enseñarte qué son los SHAP values, cómo se obtienen, los diferentes tipos que existen y cómo puedes calcularlos en Python. ¿Te suena interesante? ¡Vamos con ello!

Intuición detrás de los Shapely Values

SHAP viene de Shapely Additive Explanations, es decir, de explicar cuestiones mediante la agregación de valores Shapely. Los valores Shapely vienen de la teoría de juegos y buscan conocer cuál ha sido la contribución de cada individuo a un proceso. Por ejemplo, supongamos que dos personas se presentan de forma conjunta a un concurso y consiguen un premio de 10.000€. La forma más justa de distribuir el premio en función de la aportación de cada persona al mismo, pero, ¿cómo mides eso?

Lo ideal sería probar qué resultado hubiera obtenido cada uno de ellos por separado. De esta forma, supongamos que para distintas coaliciones (situaciones) hubieran obtenido los siguientes resultados:

Persona 1 y Persona 2 en conjunto ($C_{1,2}$): 10.000€
Persona 1 sola ($C_{1}$) 7.500€.
Persona 2 sola ($C_{2}$) 5.000€.
Si no se presenta ($C_{0}$), 0€.

El problema se refleja en la siguiente imagen de forma más clara:

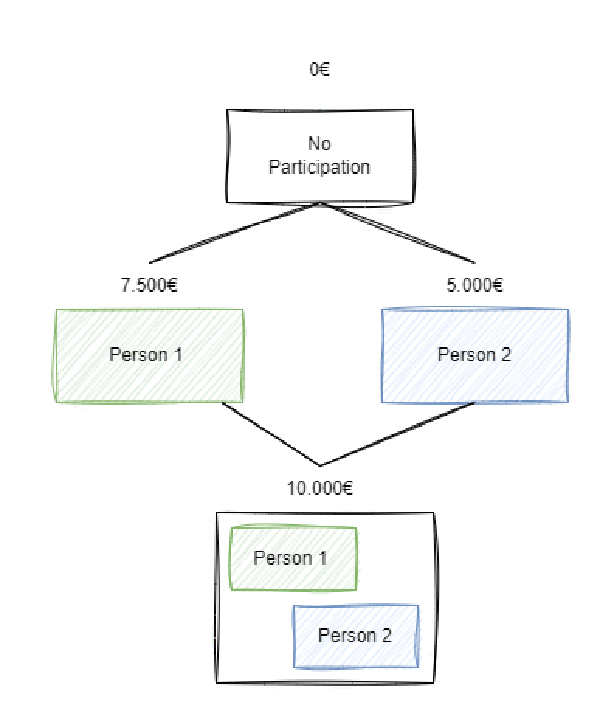
Ejemplo medición de contribución en un juego de dos personas

Así pues ¿cuánto ha contribuido la persona 1? Pues hay dos valores clave:

Si la Persona 1 no hubiera participado con la persona 2, la persona 2 hubiera obtenido únicamente 5.000€. Así pues, su contribución marginal en su coalición con la persona 2 fue de $10000 – 5000 = 5000 $.
Por otro lado, si la Persona 1 no hubiera participado hubiera ganado 0. Habiendo participado solo ha ganado 7.500€. Así pues, su contribución marginal frente a no presentarse es de $7500 – 0 = 7500$.

Por tanto, podemos decir que, de media, la Persona 1 tiene una contribución de:

$$Contrib_{Person_{1}}= \frac{7500 + 5000}{2} = 6250$$

En cambio, para el caso de la persona 2, su contribución sería la siguiente:

$$
Contrib_{Person_{2}} = \frac{(10000 – 7500) + (5000-0)}{2} = 3750
$$

Aclaración de la anotación. Cuando hablamos de la contribución de un individuo a una coalición hablamos de contribución margial (MC por sus siglas en inglés). Cuando hablamos de la contribución total de un individuo al juego, hablamos de contribució (C).

Como puedes ver, esta es una forma de distribuir el premio en función de la aportación de cada persona en el proceso. De hecho, la suma de ambas contribuciones es, en realidad, la suma total del premio ($6250 + 3750 = 10000$).

Perfecto, tenemos una forma de dividir el premio entre dos personas. Pero… la realidad es que te he hecho un poco de trampa para que sea más fácil de entender. Pensemos en otro caso, ¿qué pasaría si en vez de únicamente dos personas hubiera tres personas en el juego? Veamoslo.

Cálculo de Shapely Values para un grupo de 3 personas

Supongamos que existen 3 personas que se han presentado juntas al premio y, conjuntamente, han obtenido los 10 premios. Sin embargo, sabemos que si se hubieran presentado por separado hubieran obtenido lo siguiente:

$C_{1,2,3} = 10000$
$C_{1,2} = 7500$
$C_{1,3} = 7500$
$C_{2,3} = 5000$
$C_{1} = 5000$
$C_{2} = 5000$
$C_{3} = 0$
$C_{0} = 0$

Este caso se ve ilustrado en el siguiente gráfico:

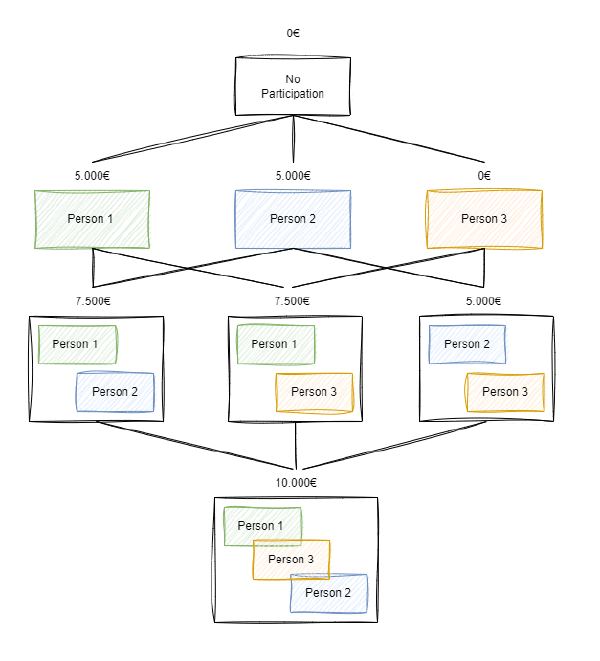
Ejemplo medición de contribución en un juego de tres personas

Si existen 3 personas, el número de coaliciones existentes crece. Si, por ejemplo, queremos conocer la contribucón de la Persona 1, ahora deberemos calcular:

La contribución marginal de la Persona 1 respecto a no presentarse. $$MC_{1} = C_{1} – C_{0} = 5000 – 0 = 5000$$
Contribución marginal de la Persona 1 en la coalición con la persona 2: $MC_{2} = C_{1,2} – C_{2} = 7500 – 5000 = 2500$
Contribución marginal de la Persona 1 en la coalición con la persona 3: $MC_{3} = C_{1,3} – C_{3} = 7500 – 0 = 7500$
Contribución marginal de la Persona 1 en la coalición con la persona 2 y 3: $MC_{4} = C_{1,2,3} – C_{2,3} = 10000 – 5000 = 5000$

Perfecto, ya tenemos las contribuciones marginales de la persona 1. Ahora hay que ponderar cada contribución marginal. La forma de hacerlo es multiplicando la contribución marginal por la probabilidad de que se dicha coalición. Veamos un ejemplo.

Pongámonos en el caso de que no se ha presentado nadie aún y que todos tienen la misma probabilidad de presentarse. Así pues, que se presente la Persona 1, la Persona 2 o la Persona 3 son igual de probables, por lo que la probabilidad de que se de una coalición de una persona, sea quien sea es la siguiente $P(C_{1}) = P(C_{2}) = P(C_{3}) = \frac{1}{3}$.

Así pues, la contribución marginal $MC_{1}$, es decir, la contribución se obtiene de la coalición solo de la persona 1 respecto a no presentarse, se debe ponderar por $\frac{1}{3}$.

¿Y para el caso de las contribuciones de la persona 1 respecto a coaliciones con una persona? En ese caso, el número de casos posibles aumentan, ya que existen las siguientes coaliciones posibles: $C_{1,2}, C_{1,3}, C_{2,1}, C_{2,3}, C_{3,1}, C_{3,2}$. Como ves, existen 6 coaliciones posibles, por lo que dichas contribuciones marginales deben ponderarse por $\frac{1}{6}$.

Nota. La coalición $C_{1,2}$ es diferentes a la coalición $C_{2, 1}$. La primera indica una coalición en la que la Persona 1 se apunta primero y la persona 2 se une a dicha coalición. El segundo caso, indica que la persona 2 se apunta primero y la persona 1 se apunta a dicha coalición. En ambos casos el resultado obtenido es el mismo, pero no es el mismo escenario.

Una forma de ver el número de coaliciones posibles es graficar contar el número de conexiones posibles entre los individuos en el gráfico anterior, tal como se muestra en la siguiente imagen:

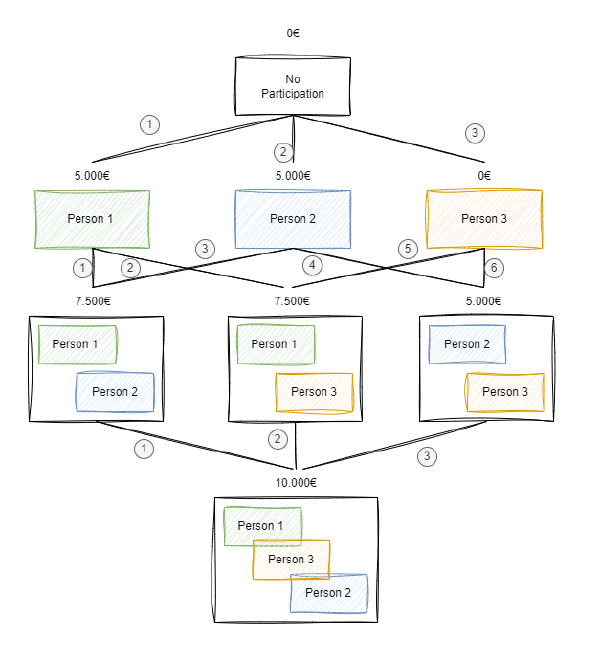
Ejemplo medición de probabilidad de combinación en un juego de tres personas

Cálculo numérico de los shapely values

Ahora que tienes la intución sobre cómo funciona, vamos a hacer los cálculos para que quede claro y afianzar las ideas.

Contribución de la Persona 1

$$Contribution_{1} = w_{1} \times MC_{1} + w_{2} \times MC_{2} + w_{3} \times MC_{3} + w_{4} \times MC_{4} = $$

$$\frac{1}{3} \times 5000 + \frac{1}{6} \times 2500 + \frac{1}{6} \times 7500 + \frac{1}{3} \times 5000 $$

$$ Contribution_{1} = 5000$$

Cotribución de la Persona 2
$$Contribution_{2} = w_{1} \times (C_{2} – C_{0}) + w_{2} \times (C_{1,2} – C_{1}) + w_{3} \times (C_{3,2} – C_{3}) + w_{4} \times (C_{1,3, 2} – C_{1,3}) =$$

$$\frac{1}{3} \times (5000 – 0) + \frac{1}{6} \times (7500 – 5000) + \frac{1}{6} \times (5000 – 0) + \frac{1}{3} \times (10000 – 7500)$$

$$Contribution_{2} = 3750$$

Cotribución de la Persona 3
$$Contribution_{3} = w_{1} \times (C_{3} – C_{0}) + w_{2} \times (C_{1,3} – C_{1}) + w_{3} \times (C_{2,3} – C_{2}) + w_{4} \times (C_{1,2, 3} – C_{1,2}) =$$

$$ \frac{1}{3} \times (0 – 0) + \frac{1}{6} \times (7500 – 5000) + \frac{1}{6} \times (5000 – 5000) + \frac{1}{3} \times (10000 – 7500)$$

$$Contribution_{3} = 1250$$

Por último podemos comprobar que los cálculos son correctos, ya que la suma de contribuciones individuales debe sumar el resultado total obtenido (10000).

Así pues:

$$Contribution_{1} + Contribution_{2} + Contribution_{3} = 10000\
5000 + 3750 + 1250 = 10000
$$

Como vemos, este sistema nos permite distribuir el premio entre diferentes participantes según el impacto de cada uno de los participantes. Ahora que ya entiendes los Shapely Values, vamos a entender los SHAP values.

Cálculo de los SHAP values en Python

Tal como indican los creadores de SHAP en su paper, SHAP viene de SHapely Addivitive exPlanations, es decir, del uso de cierta forma de los Shapely Values para la explicación de modelos de Machine Learning.

La idea es que, si queremos atribuir el impacto de cada variable en un modelo de Machine Learning, podemos tratar cada variable como un jugador, y el premio o payout como la predicción del modelo. De esta forma, podemos obtener los shapely values, lo cual nos dice cómo de importante es cada variable para obtener dicha predicción.

Así pues, el cálculo de los valores Shapely es una técnica de explicación de predicciones local, ya que explica predicciones individualizadas. Sin embargo, si agregamos las explicaciones individuales, se pueden obtener explicaciones globales del modelo. Así pues, ya vemos un punto importante, los SHAP values nos permiten tener dos tipos de explicaciones:

Las explicaciones a nivel de predicción, es decir, decir por qué un modelo ha realizado una predicción y cuánto ha contribuido cada variable en ello.
Explicaciones a nivel global, lo cual nos permite entender, de forma global cuánto impacta cada una de las variables en el modelo a la hora de obtener predicciones.

Asimismo, otro aspecto importante es que el cálculo de los Shapely values, es exponencial. Por ejemplo, si hubiera 10 variables en el modelo, habría $2^{10} = 1024$ coaliciones diferentes. Como puedes entender, estos son muchas coaliciones y supone un cálculo complejo

Tal como indican en el paper, para evitar este problema, podemos obtener unos valores aproximados de los Shapely values en lugar de tener que realizar todas las combinaciones. Existen diferentes formas de obtener dicho valor aproximado, habiendo implementaciones específicas para diferentes modelos:

Tree SHAP: es un método centrado en modelos basados en árboles, tales como el árbol de decisión, Random Forest, etc.
Expected Gradients: es un método utilizado cuando se trabaja con Redes Neuronales o modelos diferenciables.
DeepLIFT: es un método utilizado en redes neuronales, sobre todo cuando se busca entender como pequeños cambios locales en la entrada de datos afecta a la salida.
El Kernel SHAP se utiliza cuando no tenemos acceso al modelo entrenado y solo se puede acceder a las predicciones del modelo.
Partition SHAP: es útil cuando se trabaja con grandes volúmenes de datos y calcular los valores SHAP es complejo o lleva mucho tiempo.

Todo esto suena muy complejo (porque lo es). Por suerte, las personas que redactaron el paper creando los SHAP values, también crearon la librería shap de Python (enlace). Vamos a empezar por instalar la librería:

pip install shap matplotlib

Una vez instalado, la obtención de los valores SHAP es sencillo, simplemente hay que:

Entrenar un modelo (como lo harías aunque no usaras SHAP).
Crear un explainer de SHAP, el cual dependerá del tipo de modelo que hayas creado, tal como hemos mencionado anteriormente. Por ejemplo, si creas un modelo basado en árboles deberías crear un Tree SHAP explainer.
Obtener los valores SHAP con el explainer y obtener los gráficos que quieras analizar.

En el siguiente código se pone un ejemplo sencillo de funcionamiento:

import shap
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingRegressor
import matplotlib.pyplot as plt

# Load datap
X, y = load_diabetes(return_X_y=True, as_frame=True)

# Train the model
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

gbr = GradientBoostingRegressor(random_state = 1234)
gbr.fit(X_train, y_train)

# Create a SHAP explainer
explainer = shap.TreeExplainer(gbr)

# Explain the values
shap_values = explainer(X_train)

# Generate the reports
fig = shap.plots.waterfall(shap_values[0], show=False)

Ahora bien, en mi opinión lo realmente complicado es entender muy bien cómo funciona cada uno de los diferentes gráficos que puede generar SHAP. Así pues, veámoslos uno a uno:

Waterfall Plot

En un waterfall plot cada barra muestra cuánto el incremento en una unidad de dicha variable mueve la predicción hacia arriba o hacia abajo, partiendo de la media.
Un waterfall plot lo obtienes ejecutando el siguiente código:

shap.plots.waterfall(shap_values[0])

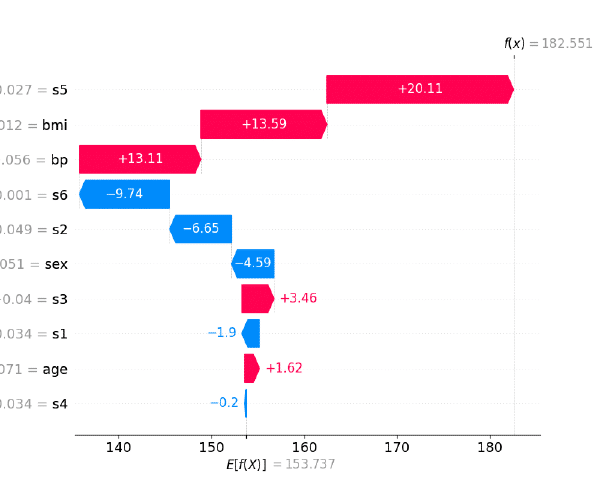
Gráfico waterfall de la librería SHAP de Python

Como vemos, partiendo de un valor medio, lo que más hace aumentar la variable a predecir (una medida sobre el progreso de la diabetes a lo largo de un año), son los incrementos en uno de las variables s5 (trigliceridos), bmi (índice de masa corporal) y bp (presión aterial).

Por el otro lado, el aumento en 1 de s6, s2 y sex (el ser hombre (0) en lugar de mujer (1)) reduce más la evolución de la enfermedad sobre la media.

Force Plot

En un Fore Plot en el centro se muestra la estimación media. Además, en rojo se muestran de forma ordenada, las variables que más impactan al incremento de la predicción (cuanto más a la derecha, más impacta), mientras que, las variables en azul muestran las variables que más impactan a reducir las predicciones de la media (cuanto mayor la barra azul, más reduce la predicción).

Aún la generación de force plots para varias observaciones con matplotlib no está permitido. Así pues, si quieres obtener el gráfico para diferentes muestras debes fijar matplotlibt = False, lo cual generará un código HTML.

Puedes generar un forceplot de una observación con el siguiente código:

shap.force_plot(
    explainer.expected_value,
    shap_values.values[0],
    X_train.iloc[[0]],
    feature_names=X_train.columns,
    matplotlib=True
)

Gráfico force plot de la librería SHAP de Python

Un uso de los forceplots es poder mostrar el impcto de las variables para distintos niveles de variables predictoras (según cuartiles, por ejemplo).

Bar Plots

El barplot obtiene el valor absoluto medio de cada columna para todas las filas, es decir, muestra cuánto afecta cada variable (en términos absolutos) al modelo. La forma de generar los bar plots es la siguiente:

shap.plots.bar(shap_values)

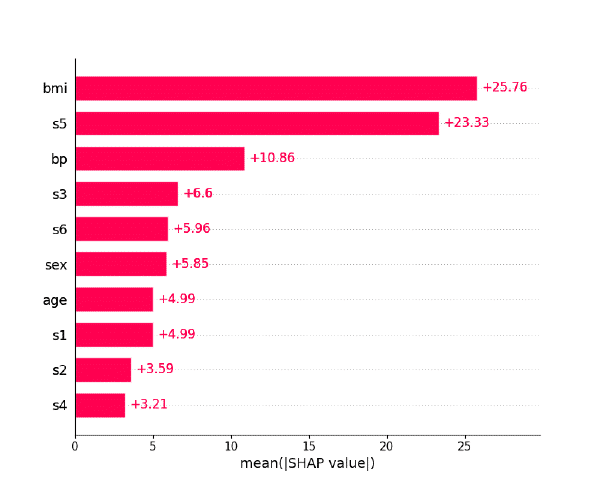
Gráfico de barras de la librería SHAP de Python

El principal problema problema de este gráfico es que, al ser valores absolutos, no indica cómo afecta (si de forma positiva o negativa).
Para ver precisamente eso hace falta o bien un waterfall plot o beeswarm plot.

Beeswarm Plots

El beeswarm plot muestra la distribución de shape values en todas las observaciones y para cada columna. Aunque es un poco más complejo de interpretar que el anterior, muestra todos los datos del dataset.
Veamos cómo se obtiene:

shap.plots.beeswarm(shap_values)

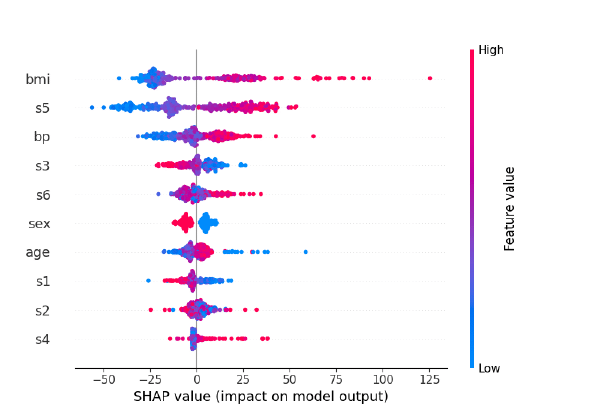
Gráfico beeswarm de la librería SHAP de Python

Conclusiones y próximos pasos

En este post te he explicado el funcionamiento de los Shapely values que resultan la base para entender los SHAP values. Además, también te he explicado cómo puedes instalar y utilizar la librería shap para obtener diferentes gráficos para interpretar mejor los modelos.

Este post no prente, ni mucho menos, ser un análisis exhaustivo de las capacidades de SHAP en la explicabilidad de modelos. Personalmente, creo que conocerlos es interesante para todo científico de datos, especialmente en esecarios donde la no introducción de sesgos, la regulación o, simplemente, el entendimiento de las predicciones obtenidas, es crítico.

Si ese es tú caso, te recomiendo que sigas investigando. En mi opinión, la mejor forma de hacerlo es profundizando con la documentación de la propia librería (enlace) y poniéndolo en práctica, así como entendiendo el funcionamiento de su código (enlace).

Además, también es importante tener en cuenta que los SHAP values no son perfectos ni la única forma de conseguir la explicabilidad de modelos. Existen otros métodos, como este de aquí.

En cualquier caso, aunque las librerías puedan ser de ayuda (siempre que se entiendan bien), la mejor forma de explicar variables es haciendo un análisis exhaustivo que incluya revisión manual y pruebas de hipótesis.

Sea como sea, espero que este post te haya servido para entender más sobre una de las técnicas de Explainable AI más conocidas y utilizadas.